Brick Walls

你需要带领一群蚂蚁去寻找食物。蚂蚁必须通过一堵相当大的砖墙。在砖块表面行走的话，容易被人们发现并被驱赶。如果他们可以通过砖块之间的缝隙行走，这就比较安全。

砖块布局如下图所示。每个砖块都是一个长为2个单位，宽为1个单位距离的矩形。在两块砖之间存在微小的缝隙（水平和垂直两个方向）。

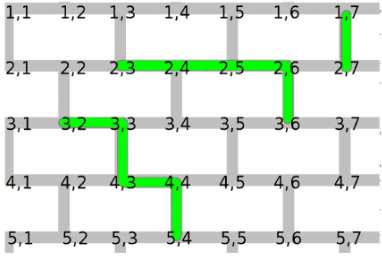
蚂蚁一开始在缝隙中的某个点，终点也是在缝隙中的某个点。假设所有砖块都是一样大小，并且是按照有间隙的规则图案排列的，因此这些点总是可以用整数坐标来表示

你的任务是找到可以从起点到终点的最短路径距离。

输入

最多存在 $ 1000 $ 组测试样例。每组测试样例由四个整数组成，其值分别为起始行 $ S_r $ ,起始列 $ S_c $ , 目标行 $ D_r $ , 目标列 $ D_c $ . （ $ 1 \le S_r , S_c, D_r , D_c \le 10^9 $ ） . 最后一行输入将是 "0 0 0 0"--这一行不得作为测试用例处理。

输出

每组测试样例对应一行最短路径距离的输出。

样例输入

样例输出

1
4
4

题目分析

目的：求出起止点之间的最短路径距离。

如果考虑将每个坐标视为节点进行建图的话，根据数值范围 $[1,10^9]$，必然是行不通的。且数值那么大考虑是否存在一定的规律。

若砖块都是 $1\times 1$ 大小的那么题目非常简单，直接求曼哈顿距离就可以了。问题在于砖块大小是 $1\times 2$ 的，给求解带来了麻烦。我们设垂直方向的距离为 disx，水平方向的距离为 disy。

画图，仔细观察，可发现只要 disx$\le$disy，那么可以直接求曼哈顿距离（如下图）。

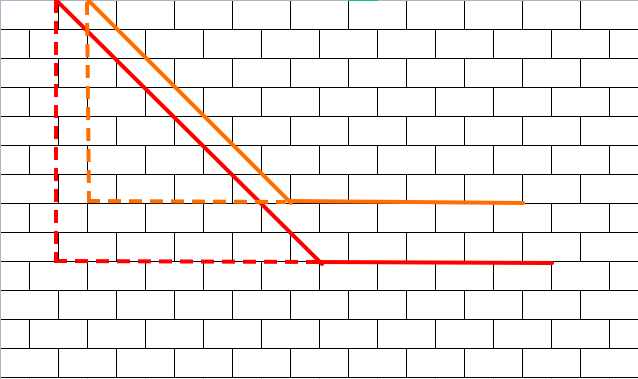
接下来考虑 disx$>$disy。

可发现，砖块的分布是呈周期变化的，且周期大小为 $2$，那么我们在找规律的时候就可以需要结合这个周期去尝试一下。

我们将行走的路线分成两个阶段，一个阶段是能使用曼哈顿距离的部分，一个阶段是不能使用曼哈顿距离的阶段。

对于第二个阶段，又能分两种情况，一是有直接往下走的缝隙，二是没有直接往下走的缝隙。对于情况一的特征判断就是只要起点的横纵坐标奇偶性一致，第一阶段结束了，就有直接往下的道路。否则，就没有属于情况二。

对于数值方向上行走的距离，可发现无论哪种情况，都是坐标差值，难点在于水平位置上需要来回着进行行走。那么观察下不同垂直距离对应的来回行走的距离情况。

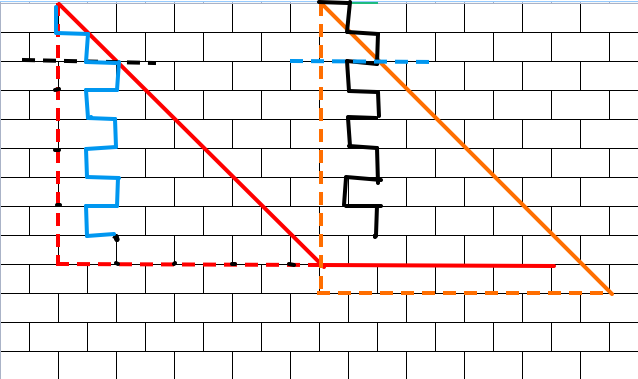
情况1		情况2
垂直距离	来回行走距离	垂直距离	来回行走距离
$1$	$0$	$1$	$2$
$2$	$2$	$2$	$2$
$3$	$2$	$3$	$4$
$4$	$4$	$4$	$4$
$5$	$4$	$5$	$6$
$6$	$6$	$6$	$6$
$7$	$6$	$7$	$8$
$8$	$8$	$8$	$8$

可发现是呈存在变化规律的，那么分情况进行讨论即可。

代码实现

#include <bits/stdc++.h>
using namespace std;
int sx,sy,fx,fy;
typedef long long ll;
int main()
{
    while(cin>>sx>>sy>>fx>>fy&&(sx||sy||fx||fy)){
        ll disx=abs(sx-fx),disy=abs(sy-fy);
        ll ans=0;
        if(disx<=disy) cout<<disx+disy<<endl;//曼哈顿距离
        else{
            if(sx>fx){//调整位置，保证从上往下
                swap(sx,fx);
                swap(sy,fy);
            }
            ans=disx+disy;//计算阶段1 + 阶段2的垂直部分距离 (disy+disy)+(disx-disy)
            disx-=disy;
            //判断是否属于情况1 坐标奇偶性相同
            if((sx%2!=0&&sy%2!=0)||(sx%2==0&&sy%2==0)){
                ans+=disx/2*2;
            }else{//情况2
                ans+=(disx+1)/2*2;
            }
            cout<<ans<<endl;
        }
    }
    return 0;
}

Brick Walls